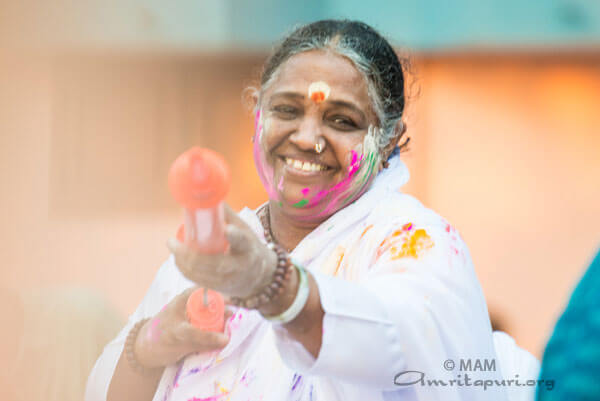-

Fulfill our responsibilities to Bharatamba
Today we commemorate the complete freedom that India attained. Today is the anniversary that we got our own Constitution and…
-

Innovation & Research awards honor outstanding faculty
Even if you are not able to see anything, don’t lose your confidence in your research work; keep doing, keep…
-

Akshata from Ram Mandir offered to Amma
Heaven is on earth itself, not anywhere else. We can only enjoy it if we sustain Dharma. Sri Rama embodies…
-

Those who bring solace to the suffering are true lovers of God
Amritapuri transformed into a melting pot of cultures for its Christmas celebrations. The program unfolded with a diverse array of…
-

Gita Jayanthi celebrations illuminate Ashram with art & wisdom
Devotees and artists alike gathered to immerse themselves in the profound teachings of Gita. Gita chanting, Gita talks, and a…
-

Amma bestows blessings on Shadadhara Pratishta
14 Dec 2023, Amritapuri Ashram In a touching display of devotion and community support, Amma graced a simple ceremony at…
-

Bharat is the land that has taught the world the ultimate truth
Amma graced the World Hindu Congress with her presence. The quadrennial event, brings together over 2400 delegates from more than…
-

Mentally challenged students redefine the essence of education and living
Beyond the talents displayed, what stood out most was the evident love and care the students had for each other.…
Amma’s desire
Amma has a desire. Everyone in the world should be able to sleep without fear, at least for one night. Everyone should be able to eat to his or her fill, at least for one day. There should be at least one day when hospitals see no one admitted due to violence. By doing selfless service for at least one day, everyone—from little children to the very elderly—should help raise money for the poor and needy—even if by making toys. It is Amma’s prayer that at least this small dream be realised.

Amrit Ganga: Beautiful moments from Amma’s life, Darshan, Yatra, Satsang & Bhajan. Weekly episodes.
From Amma’s Heart: Discover the profound wisdom of Amma Mata Amritanandamayi Devi in this enlightening video.
Interesting Articles from the Archives
-
Historic and unique Gita Jnana Yajna concludes
One-year-long Bhagavad Gita Jnana Yaga (700 speakers in 10 languages, from 25 countries, age 8-84, 31 Sannyasis, 311 Brahmacharis, 160 Internationals, 32 kids) concluded
-
What is real prayer? A lesson from Ramayana month
The test was simple but demanding: whoever could lift and string the mighty bow of Shiva, a gift to King Janaka, would win Sita’s hand in…
-
Holi, the Festival of Colours, Joy and Renewal
Holi was Krishna and the gopi’s celebration of Love. This teasing, affectionate panorama of feeling and colour has been captured